Simulation Topics¶
Physically Based Simulation¶
At its core, Ziva VFX is a physically based simulator. As input, it takes a complete description of the physical setup of the scene, including: materials, tissue volumes, bone motion, attachments between objects, gravity, etc. This is what you must provide when setting up a scene with Ziva VFX. From that input, it computes motion of tissues and cloth based on laws of physics. This is a fully-coupled interaction of all properties of the system at once.
Technical Details¶
The elastic materials are modelled with the finite element methods (FEM). For a more technical introduction to FEM, see http://www.femdefo.org.
The solver uses implicit time integration with all force terms formulated implicitly. Implicit integration can handle stiff materials and attachments with large timesteps.
Quasi-Static Solving¶
The solver normally operates in dynamic mode: it calculates deformable dynamics (wave propagation, transient effects, oscillation, bouncing) of the simulated objects. It is possible to turn dynamics off, and use the quasi-static mode. In this mode, the bodies have no momentum and remain in a state of internal equilibrium. Quasi-static mode is useful for situations where dynamic effects are not desirable, such as when using simulation outputs to create blendShape targets.
When using quasi-static simulation mode, it is important to have enough fixed attachments for the solve to converge. The number of fixed attachments will change depending on a variety of factors. For anatomical simulation, this limitation does not pose a problem, as biological tissues will typically have many attachments.
Simulation Objects¶
Bones¶
Bones are externally animated Maya meshes of any geometry and purpose whatsoever. The Ziva solver does not simulate the bones or modify their motion in any way. The bones may deform and/or be animated using any Maya technique. The “bone” surfaces are not restricted to represent biological bones, but can be the result of any transformation or deformation in your Maya session (skin cluster, keyframe animation, loaded from an Alembic bake, any Maya deformer).
One common use it to have bones come from a previously baked simulation run. This makes it possible, say, to bake the result of a previous simulation as a deformable “bone”, and then constrain the next simulation layer to it, using Attachments. In this way, one can progressively generate an animation, by layering the muscles, fat, skin, etc. Each of these layers can be a separate solve with the result of the previous layer treated as a deformable bone for the next layer.
Cloth¶
Cloth models thin objects (represented with a triangle mesh), for example: sheets, cloth, membranes. Cloth is simulated using the Ziva solver. As of version 1.0, cloth is suitable for simulation of fascia and skin, but may not be appropriate for clothing because it lacks a self-collision model.
As of version 1.1, cloth supports two new features: rest scale and pressure. Rest scale (zMaterial.restScale) makes it possible to shrink or enlarge the rest state of the cloth. This parameter can be painted spatially. A value of 1.0 means no scaling, which is the default. For example, to make the fascia cloth mesh wrap tightly around muscles, set zMaterial.restScale to 0.9. Rest scale can be animated over time using zCloth.restScaleEnvelope. This can be used, for example, to ramp up the effect over a few frames, rather than insert it abruptly in one frame. A value of 1.0 means that the scaling effect is fully applied, whereas 0.0 means that it is turned off. In-between values partially apply the effect. Negative values reverse the effect, and values greater than 1.0 exaggerate the effect. Pressure (zMaterial.pressure) applies external pressure to the cloth. This makes the fascia cloth fill-in any little valleys in between the muscles, which makes the muscle geometry more pronounced in the fascia. Pressure is given in N / m^2. A value of 0.0 means no pressure. Positive values mean that the pressure is trying to compress the volume enclosed by the cloth, and negative values mean that it is trying to expand it. A value of 1.0 has no special significance; it is common to set values such as, for example, 100.0. The pressure can be animated over time using zCloth.pressureEnvelope. This parameter behaves in a manner analogous to zCloth.restScaleEnvelope.
A demonstration of cloth restScale and pressure is available in the Built-in demo “Cloth Rest Scale and Pressure” (on the Ziva Tools menu).
Tissue¶
Tissues are three-dimensional solid deformable objects. Tissues can be used to simulate biological solids like: muscles, fat, or skin. They can also be used for non-biological materials like: jello, rubber tires, foam blocks, and steel beams.
Subtissues¶
A subtissue defines material properties, muscle fibers, and attachments within another tissue. A subtissue does not appear as its own tet mesh in the physical simulation. This can be useful for a few different applications. The right way to think of subtissues are as a sort of inclusion in the parent tissue.
Subtissues can be a tool for specifying material properties on the interior of a mesh. While material properties are normally smoothly interpolated through the volume of a tissue, one can use a subtissue to specify a discontinuous change to different material properties in the middle of an object. For example, perhaps there is a stiff knot in the middle of a muscle.
Subtissues can be used to model muscles embedded in passive tissue. For example, an entire arm could be simulated as a single tissue, with the individual muscles acting as subtissues. Their contractions and different stiffnesses will affect the single parent tissue without simulating separate tet meshes.
Subtissues can be used to group together adjacent muscles into a single simulation object. This could provide a performance improvement if it uses fewer tets. It could also make rigging easier, as collisions and attachment between these muscles does not need to be setup. Since they are in the same object, that is all implicit. They will not slide relative to each other or penetrate.
Attachments¶
The tissues, cloth, and bones can be connected to each other (constrained) with attachments. Any type of object can be attached to any other type of object, with the exception of bones to other bones. Bone-to-bone attachments are not included because bones are not simulated by Ziva VFX and hence such attachments would have no effect. Each attachment can be fixed (pinned) or sliding (free to move over a surface).
When attaching between two bodies, the order matters. The first object is the source and the second object is the target. When an attachment is created between two bodies, the vertices of the source object “reach out” to the target object and attach to the closest point on the target.
The “stiffness” attribute controls how much the attachment between the bodies can stretch. The stiffness can be further attenuated by painting the attachment weight between 0-1 on the source mesh. For sliding attachments, painting on the target mesh controls where the attachment is allowed to slide. It will not slide to an area painted with zero weight.
In practice, one often wants to attach a set of model vertices to another model. This can be achieved by painting an attachment weight of 1 at these vertices and a 0 weight at all the other vertices. In order to facilitate this process, the user can select the vertices using the Maya UI, selecting the other object, and creating an attachment. The attachment weights will be painted automatically.
Each attachment also has an option to set it to “hard”. This does not change the stiffness or behaviour of the attachment or dynamics. It changes the internal algorithm used when solving this attachment to one that is more appropriate for very stiff attachments, but usually runs slower. This option is not normally needed, but if instabilities (oscillations or explosions) are observed on an attachment with very high stiffness, then checking this option may improve the behaviour.
A demonstration of attachments is available in the Built-in demo “Attachments” (on the Ziva Tools menu).
Goaling Attachments¶
Goaling attachments exist to make mesh A follow (“goal”) an arbitrary (externally prescribed) animation of a mesh B with the same mesh connectivity. The motion of the goaled mesh A is solved with the Ziva solver. It obeys physics, while being constrained to follow the goaled mesh B. The result is a compromise between physics and following the goaled mesh animation. Typically, the goaled mesh animation will be generated by artists using any Maya technique, for example, keyframe animation or standard skinning. The Ziva goaling attachment is then used to add “physics” to the animation, providing a compromise between physics and artist directability.
The goaling mesh A must be a Ziva tissue, and the goaled mesh B must be a Ziva bone. The two meshes must have the same number of vertices, ordered in the same way. The strength of the goaling can be adjusted using the zGoalAttachment.strength attribute, and permits to adjust the tradeoff between following physics versus the goaled bone motion. This attribute can be painted spatially, making it possible to turn off goaling in selected regions, or weaken/strenghten it arbitrarily.
A demonstration of goaling is available in the Built-in demo “Goaling, Self-Collisions, Ziva Cache and Spatially-Varying Materials” (the “fish” demo; on the Ziva Tools menu).
Collisions¶
To enable collisions, there is a “collisionDetection” attribute on the zSolver node. There are also per-body collision attributes on the zTissue, zCloth, and the zBone nodes. Like attachments; collision response can be Soft or Hard, and Fixed or Sliding.
Two bodies can only collide if at least one of them has “collisionVolume” turned on. Unless a mesh is closed and watertight, the “collisionVolume” attribute doesn’t make sense and shouldn’t be turned on. If it is turned on for a non watertight, it may or may not work properly.
When two bodies interact, the body with the more stable and/or restrictive collision response settings defines the interaction. When two bodies collide, the effective collision stiffness is a blend between the setting from the two objects. When a sliding contact interacts with a fixed contact; the interaction will be “fixed”. If a soft contact interacts with a hard contact; the interaction will be “hard”.
The “collisionPointSpacing” attribute on the solver can sometimes be very important. Collisions are processed on a point-by-point basis, starting with the vertices of the triangle meshes use to make the objects. Sometimes this is not enough resolution to captures the collisions, in which case additional points can be added during collision handling by setting “collisionPointSpacing” to the desired distance between adjacent collision points. Be aware that setting this parameter too small can easily generate a tremendous number of points, which will slow the solver down significantly. This can happen with the default settings, if your objects are very large. During a collision, the collision points are rendered in the Maya viewport, so the collision spacing can be seen.
A demonstration of collisions is available in the Built-in demos “Self-Collisions, Ziva Cache and Delaunay Tet Mesher” and “Collisions” (on the Ziva Tools menu).
Real World Units¶
Ziva VFX uses real-world scientific units for most parameters:
| Value | = Units |
|---|---|
| Lengths | = meters [m] |
| Times | = seconds [s] |
| Masses | = kilograms [kg] |
| Material stiffness | = N/m 2 = Pa = kg/(s 2 m) |
| Fiber strength | = N/m 2 |
| Attachment stiffness | = N/m 3 |
| Density | = kg/m 3 |
Real world values are available for many materials, such as on Wikipedia and other sources.
Elastic Materials¶
A material refers to the physical properties of a tissue or cloth. This includes simple properties like density, which affects mass and inertia. It also includes more complicated material properties, such as the model of the relationship between strain (essentially displacement) and stress (essentially elastic forces). The general form of the relationship is determined by the material type, whereas the overall magnitude of the forces that the material experiences under the deformations is controlled by the stiffness and other numerical parameters. Ziva VFX provides a choice of elastic material types for tissues: StVK, neo-Hookean, co-rotational and anisotropic. For cloth there is only one model type present. These material types are common in computer graphics and engineering, although the details are different.
Stiffness¶
The stiffness (how hard or soft it is) of a tissue or a cloth is controlled by adjusting the Young’s modulus parameter on the zMaterial node. This is the standard way real-world stiffness is measured in science and engineering and the values for many real materials are available. Example Young’s moduli:
| gelatin | 1.0 * 10 0 = 1 |
| brain | 0.5 * 10 3 = 500 |
| liver | 0.7 * 10 3 = 700 |
| breast tissue | 0.9 * 10 3 = 900 |
| fat | 3.0 * 10 3 = 3,000 |
| smooth muscle | 5.0 * 10 3 = 5,000 |
| skeletal muscle | 1.2 * 10 4 = 12,000 |
| cartilage | 2.0 * 10 4 = 20,000 |
| rubber | 1.0 * 10 7 = 10,000,000 |
| wood | 0.6 * 10 9 = 600,000,000 |
| tendon | 1.0 * 10 9 = 1,000,000,000 |
| plastic | 1.5 * 10 9 = 1,500,000,000 |
| bone | 1.4 * 10 10 = 14,000,000,000 |
| walnut shell | 1.5 * 10 10 = 15,000,000,000 |
| steel | 2.0 * 10 11 = 200,000,000,000 |
| diamond | 1.0 * 10 12 = 1,000,000,000,000 |
Young’s moduli for various materials [N / m 2]
Material Types¶
StVK Material¶
The Saint Venant–Kirchhoff (StVK) generally gives good visual results, and is our default material. This material becomes more and more stiff as it stretches, which is often useful in practice as it reduces excessive stretching. StVK and NeoHookean materials have an additional parameter: compression resistance. This important parameter controls the tissue’s volume preservation under large deformations. See more comments below, under Volume Preservation.
Neo-Hookean Material¶
Neo-Hookean materials do not become progressively stiffer under stretching, unlike StVK. This is a popular class of solid materials in engineering. They are often used to model rubber.
Co-rotational Material¶
The corotational material is a linear tissue material capable of resolving large rotations + a small amount of deformation applied on top of the rotation. One can apply large deformations too, but the material will visibly stretch/compress with little resistance (linearly), and without preserving volume. This material is very popular in computer graphics and engineering – it is used in many research papers and commercial systems. In comparison to StVK, this material is about 10% faster, but StVK generally looks better under large deformations.
Anisotropic Material¶
This gives a tissue material that is weaker (or stronger) in a plane orthogonal to the given specified anisotropic direction. The anisotropic direction can vary spatially, and is specified via the muscle fiber field. The relative strength of the orthogonal direction (transverse anisotropy) is specified in the zTissue node, and can assume any positive real value. A value of 1.0 gives an isotropic material, values less than 1.0 gives materials that are weaker in the orthogonal direction, whereas values greater than 1.0 give materials that are stronger in the orthogonal direction.

A tissue sphere is suspended under gravity and attached to two bones (the two cones). Both the isotropic and anisotropic materials use the same scene parameters. The anisotropic material is 20x weaker in the direction orthogonal to the red fiber field (red). As a result, a visible bulge forms in the anisotropic material.
Cloth Material¶
The cloth in Ziva VFX is based on the “Baraff-Witkin” cloth model, as described in by D. Baraff and A. Witkin at SIGGRAPH 1998, but with a custom model for bending energy. The cloth material is controlled by prescribing its tensile, shear and bend strengths. The tensile strength controls how much the cloth resists tension or compression, shear strength controls how much the cloth resists shear, and bend strength controls how much the material resists bending. The neutral bending angle can either be zero (flat) or the angles in the input mesh.
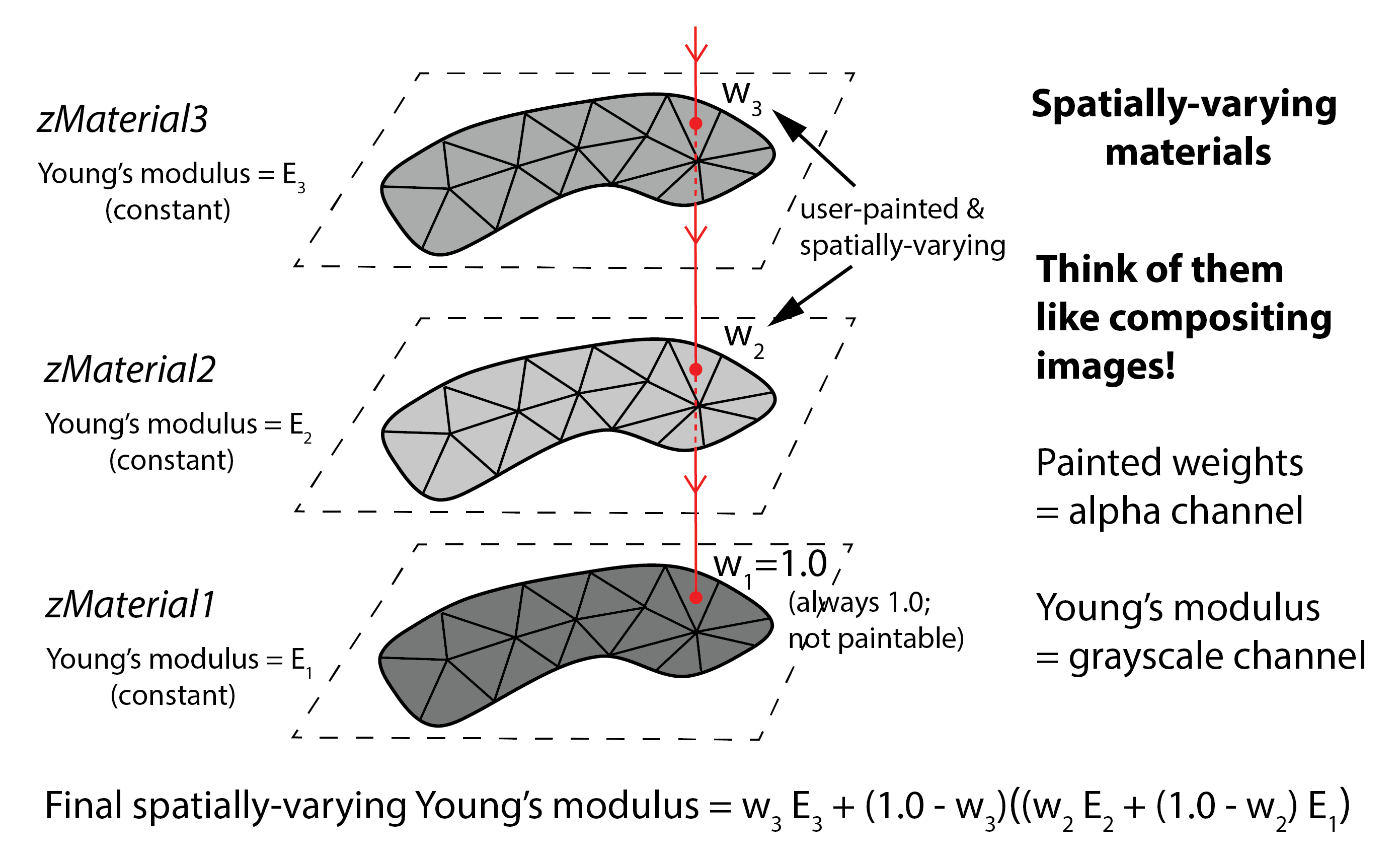
Layering and Blending Materials¶
All of the material properties defined on the zMaterial node (e.g. stiffness, volume preservation, and density) can be made to vary across the elastic object. This is done by using multiple zMaterial nodes on the same object (see Figure). Each zMaterial node defines a uniform homogeneous material, but the paintable zMaterial.weights is used as an ‘alpha mask’ to composite the material layers together. The earlier materials in the dependency graph are effectively over-written by later materials when the weight map is non-zero. The first zMaterial on each object must have weights=1, because there is no lower material layer to blend with.
For example, to make a solid ball whose left side is 10x stiffer than the right side, assign the default Young’s modulus to the base material (zMaterial1). Then, create a new material (zMaterial2), and assign 10x stiffer Young’s modulus to it. Then, paint the value of 0.0 onto the right side of the sphere for zMaterial2.weights, but leave the weights as 1.0 on the left side of the sphere.
The spatially-varying maps are painted on the triangle-mesh surface, via zMaterial.weights. These surface maps are smoothly extended into the volume before simulation begins, and then transferred on to the tetrahedral mesh. If the tet mesh resolution is significantly lower than the size of the painted features, then those material details will not be visible in the simulation.
While the material values may vary across each object, individual objects must be assigned only one material type (e.g. StVK, co-rotational, NeoHookean or Anisotropic). Different objects in the scene can have different types.
A demonstration of spatially-varying material is available in the Built-in demo “Spatially Varying Materials” (on the Ziva Tools menu).
Volume Preservation¶
Volume preservation is visually important for the simulation of solids (tissues). Our plugin offers multiple ways to control tissue volume preservation. First, there is the Poisson’s ratio parameter. Poisson’s ratio defines the relative change in volume under material stretching and successfully controls volume preservation under small deformations. Mathematically, it does not apply to large deformations, although it is often used in practice for that purpose also. Values near 0.5 cause the simulated material to act unnaturally stiff, so we don’t recommend putting Poisson’s ratio too high (e.g. stay below 0.45).
Under large deformations, our plugin can preserve volume via the volume conservation parameter. The higher this setting, the more the tissue preserves volume. Alternatively, the compression resistance parameter can be used to prevent compression, but permit expansion.
The compression resistance strength scales with Young’s modulus (stiffness) and typical effective values are in the 100’s and 1000’s, occasionally up to 10,000 or higher. The volume conservation parameter is independent of Young’s modulus, and typical effective values may be 10 2 to 10 7 times larger than Young’s modulus.
Large values for compression resistance may cause simulation instabilities requiring more substeps or Newton iterations to resolve. The volume conservation setting is typically more stable.
Using volume conservation or compression resistance makes it possible to simulate very soft materials. For example, try decreasing Young’s modulus to a very small value. With a sufficient level of volume conservation or compression resistance, you should see soft, goop-like behavior.
Muscle Fibers¶
Adding a muscle fiber (the zFiber node) to a tissue allows it to contract like a real muscle. When excited (excitation > 0), the muscle will contract along the direction of its fibers, which are shown in the viewport. The fiber direction is controlled by painting the endpoints to 0 and 1 on the endpoint map. The fibers flow smoothly between the endpoints. The strength of the muscle controls how much it contracts and can be painted across the surface of the mesh.
The fiber will not contract past contractionLimit times its initial length. If contractionLimit is set to 0.5, then the muscle will attempt to contract to half its length. The elastic material will resist this contraction and its actual contracted length will be somewhere in between. If contractionLimit is set to 1.0, then the muscle will not contract at all, but excitation will make the material more stiff.
The excitation of each zFiber can be key-framed, allowing muscle contraction to be directly and artistically controlled. For a semi-automatic muscle excitation, a “line-of-action” can be added to each zFiber node. The line of action requires one or more curves as input, and it excites the muscle when the curve gets shorter. This still requires animating the curve with traditional rigging techniques, but then key-framing the excitation is unnecessary (though still possible). We find that a simple skin cluster is sufficiently good for rigging the line-of-action curve. The initial creation of a very simple curve can be done automatically with the zLineOfActionUtil command.
More than one fiber node can be added to the same tissue. They can all have different parameters and excite and contract independently.
Tetrahedal Meshes¶
The simulation of tissues internally operates on tetrahedral (tet) meshes. The tet mesh acts as a ‘cage’ that controls how the muscle can deform and is a key requirement to get right in a simulation.
Lattice Tet Meshes¶
Our primary tet meshing approach is based on an adaptively refined regular lattice. This is controlled through the zTet node that’s created with every tissue.
A higher resolution tet mesh will allow more detailed deformations, but it will run slower. The single parameter ‘tet size’ sets the global maximum size that a tet can be anywhere in the volume. Starting with default parameters, changing ‘tet size’ is a natural place to start tweaking the resolution.
The resolution can also be spatially-varying across the surface and through the volume. To adjust the resolution across the surface of the tissues, paint the ‘weights’ map and adjust ‘surface refinement’. The resolution on the interior of the volume is a blend between the global ‘tet size’ and the surface resolution. ‘Refinement propagation’ controls the influence how much the surface resolution influences the interior.
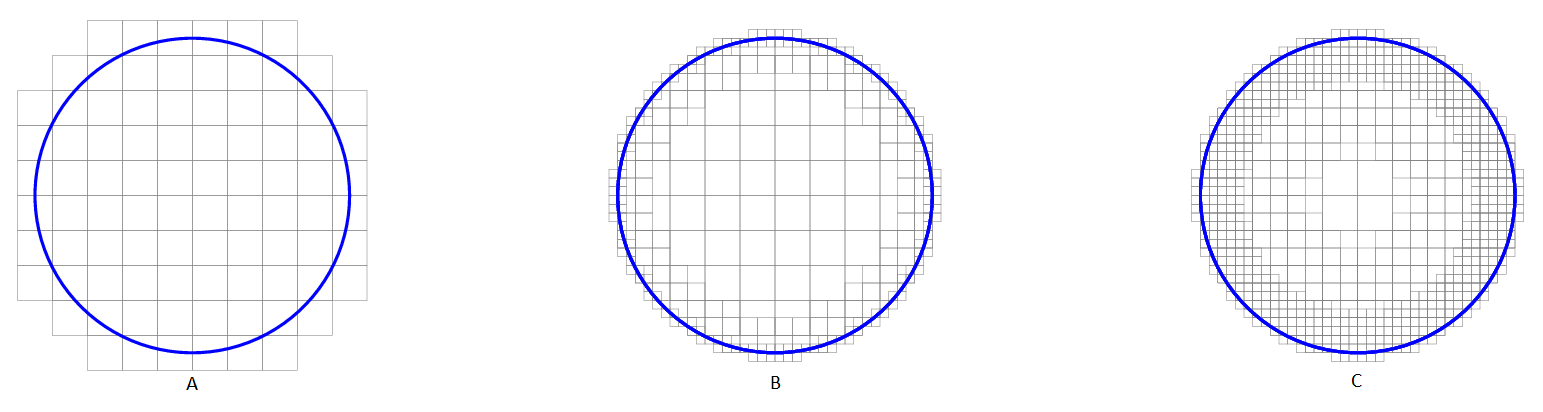
Effect of “surface refinement” and “refinement propagation” on tet meshing on a 2D example. The circle represents the triangle mesh surface of the tissue. The grid represents the generated tet mesh. (A) Surface refinement set to zero, and refinement propagation are set to zero. (B) Surface refinement set to two, and refinement propagation set to zero. (C) Surface refinement set to two, and refinement propagation set to half. This example is in 2D with quad-meshes, the behaviour with 3D tet meshes is analogous.
The tet mesh can cover different parts of the volume of the given surface by changing the ‘fill interior’ parameter. The style should be chosen to best cover the region that is intended to be solid material. The “Empty Cavities” option is most likely the correct choice, but it requires watertight input meshes to work. It does not make sense with arbitrary meshes full of holes and intersections, for which “Filled Cavities” is probably the correct choice. The “Surface Only” option covers only the input triangle mesh. This is sometimes useful, but switching to cloth is often the more appropriate choice.
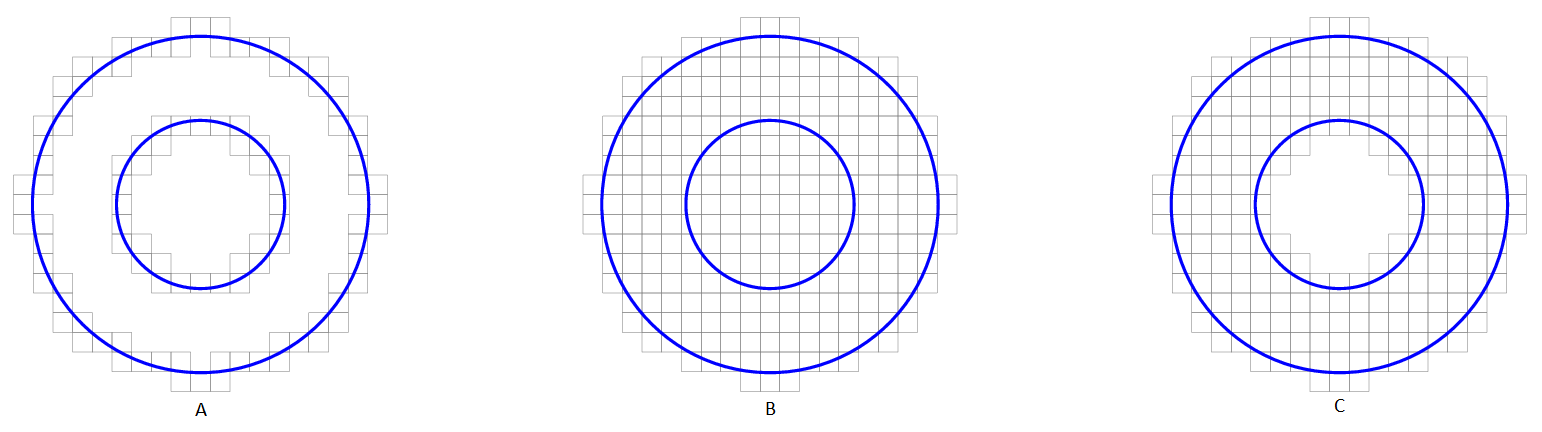
Effect of “fill interior” on tet meshing on a 2D example. The circle represents the triangle mesh surface of the tissue. The grid represents the generated tet mesh. (A) Surface Only. (B) Filled Cavities. (C) Empty Cavities. This example is in 2D with quad-meshes, the behaviour with 3D tet meshes is analogous.
Delaunay Tet Meshes¶
Delaunay refinement is an alternative approach to creating tet meshes, available through the zDelaunayTetMesh node. This strategy is less controllable and less reliable than the lattice-based tet meshes, but produces tet meshes that exactly match the shape of a given triangle mesh. This property is sometimes useful, but is not required for a high-quality simulation.
The input to this node must be a quality manifold surface mesh. Meshes produced by the zIsoMesh node generally form good inputs to the zDelaunayTet node. The refinementQuality parameters controls the amount of mesh refinement. Valid values are in the 0 to 1 range. A value of 0.0 means no refinement, whereas 1.0 means high-quality refinement. It is recommended to keep this parameter at a value of 0.8 or higher.
Embedding Meshes into Tissues¶
The tissues in our system are simulated as tetrahedral meshes. When you generate a tissue, its triangle mesh is automatically embedded into the generated tet mesh. Additional Maya triangle meshes can be embedded into our tissue tet mesh, allowing you to easily update your simulation, say, if the triangle model is refined at a later stage in the production. Our attachments, collisions and space-varying coefficients are authored on triangle mesh geometry. Our solver then transfers these values to the tissue tet mesh. As a result, the editing of volume data is no more difficult than painting the weights for a skinCluster.
Damping¶
Damping is the mechanism by which objects lose energy and slow down. Our plugin provides two kinds of damping, both adjustable in the solver node. “Stiffness damping” primarily dampens high-frequencies (rapid vibrations, in space and/or time). It is useful to increase stability without damping the simulation too much. “Mass damping” is a non-physical damping, somewhat like being under water. It slows all motions equally. We usually set “mass damping” to zero, and use a small amount of “stiffness damping”. Note that you definitely need a small amount of damping to keep the simulation stable.
Inertial Damping¶
Inertial damping is a non-physical effect useful to enhance stability or handle non-physical inputs. Inertial damping prevents tissues from ‘feeling’ inertia due to large-scale motions (all affine modes: translation, rotation, shear, and scale). Tissues with inertial damping have no momentum from these modes. The tissue effectively acts like a quasi-statics for these modes, but normal dynamics for higher-frequency components. Small-scale deformations still have all of their inertia, so elastic waves travel through objects normally. Using this, tissues can be subjected to extreme acceleration without flying themselves apart. Enable this on the zTissue node. This is very different from the mass and stiffness damping available on the zSolver node. We prefer to leave this turned off until we see a specific need for it.
Animatable Inertial Frame¶
The solver node can be transformed / animated using its translate, rotate and scale attributes, in the usual Maya fashion. If the solver node, and the bones of a creature, are transformed in unison, the space that the tissues or cloth are being solved in, will rigidly transform with the solver, canceling any inertial effect due to bone motion. This is useful for moving simulations away from origin without incurring inertial effects.
Isosurface Triangle Mesh Creation¶
We can create well-conditioned triangle meshes using our Isosurface Triangle mesh generator. We use a level-set-based approach and 3D Delaunay meshing. The input is an arbitrary Maya polygonal mesh that does not need to be closed, manifold or well-formed. It can have cracks, duplicate faces, T-vertices, etc. The output is a 3D triangle re-meshing of the same surface, or an offset surface. For the offset, both positive, zero and negative values are supported. The re-mesher can also remesh triangular meshes that do not enclose any volume – in which case the provided offset must be greater than zero.
All the angles in the output triangulation are equal or greater than 30 degrees (unless manifoldness of the output surface is enforced, below). The output of this node is a Maya mesh. As such, it is independent of our solver, and can be used for any purpose in Maya.
The re-mesher does not assume that the input mesh is manifold or well-formed. It can work with arbitrary “polygon-soup meshes”, including one-sided surfaces and surfaces with holes. The remesher can be used to fill holes in non-watertight geometry and to create a good-looking surface matching the input geometry. In the context of our plugin, the remesher can be used to create a well-formed mesh to serve an input to tissue creation. The output of this node also provides a good starting point for Delaunay Tetrahedralization. The parameters to the remesher are the level-set value to mesh (the “isoValue”), the target size of the output triangles, and the level-set resolution.
The isoValue is specified in scene units, and can be positive, zero, or negative. Zero and negative values only make sense when the input object represents a solid volume. In such cases, the zero isosurface will effectively remesh the input surface. A negative value will effectively “shrink” the object, whereas a positive value will enlarge it. If the input is not a closed volume, then the zero (or negative) isosurface will be empty.
The triangle size is specified in dimensionless units, where 1.0 is a default triangle size. This parameter controls the size of the output triangles. For example, if you set it to 2.0, you can expect the output triangles to be approximately 2x larger than with 1.0. The larger the value, the coarser the mesh. Conversely, the smaller the value, the smaller the mesh, and the longer the running time.
The resolution controls the resolution of the internal level set representation. This controls what geometric features are visible to the method. Increasing the resolution will cause the output mesh to respect input detailed features more closely, at the cost of more memory and computation.
In many cases, the output of the remesher is a manifold surface. When it is not, the produceManifoldMesh parameter, if enabled, applies a post-processing step that attempts to make the mesh manifold by removing hanging faces and performing edge collapses. You can disable this post-processing by turning produceManifoldMesh off. The Delaunay 3D tet mesher needs a manifold mesh as input.
A demonstration of isomeshing is available in the Built-in demo “Isomesher” (on the Ziva Tools menu).
Thread Management¶
Our solver automatically uses threading to accelerate the computation. The amount of threading is controlled using the Maya multithreading settings (e.g. the threadCount command). The mesh and the problem must be sufficiently large (e.g., at least a few hundred tets) to see any advantage from multithreading.